3D Configuration Space

As you saw, the configuration space for a robot changes depending on its rotation. Allowing a robot to rotate adds a degree of freedom - so, sensibly, it complicates the configuration space as well. Luckily, this is actually very simple to handle. The dimension of the configuration space is equal to the number of degrees of freedom that the robot has.

While a 2D configuration space was able to represent the x- and y-translation of the robot, a third dimension is required to represent the rotation of the robot.

Let’s look at a robot and its corresponding configuration space for two different rotations. The first will have the robot at 0°, and the second at 18°.

A three-dimensional configuration space can be generated by stacking two-dimensional configuration spaces as layers - as seen in the image below.

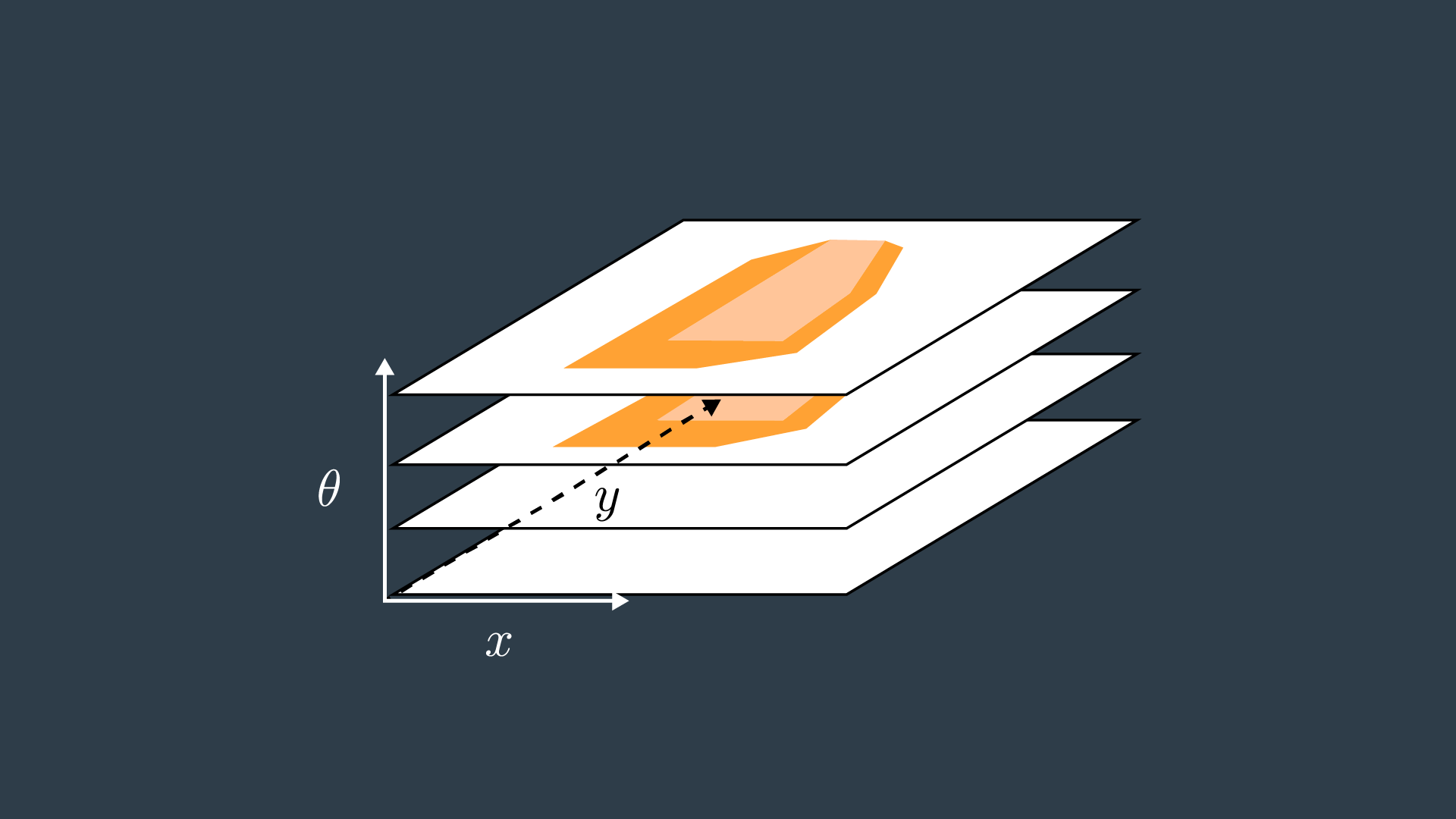
If we were to calculate the configuration spaces for infinitesimally small rotations of the robot, and stack them on top of each other - we would get something that looks like the image below.

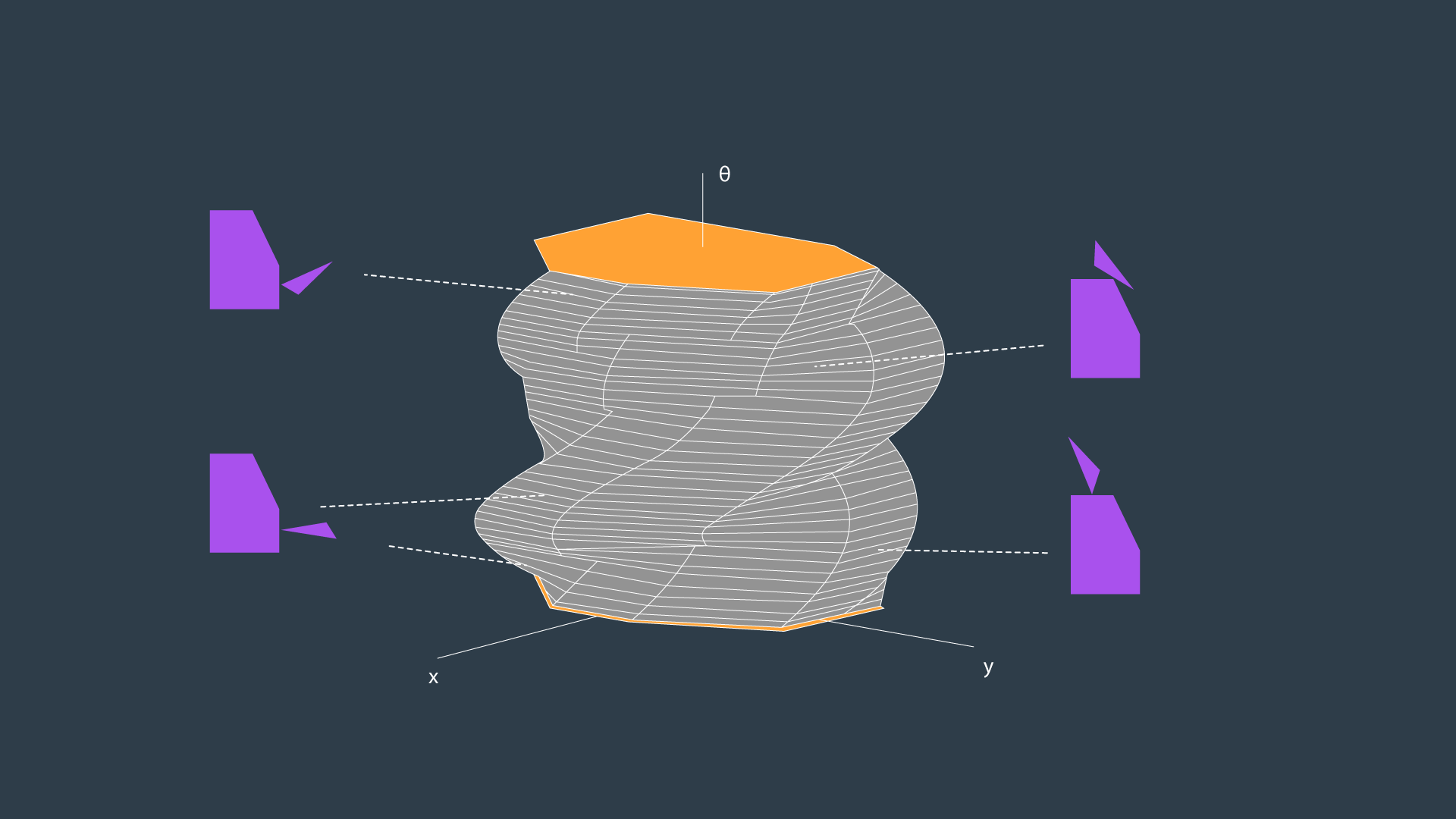
The image above displays the configuration space for a triangular robot that is able to translate in two dimensions as well as rotate about its z-axis. While this image looks complicated to construct, there are a few tricks that can be used to generate 3D configuration spaces and move about them. The following video from the Freie Universität Berlin is a wonderful visualization of a 3D configuration space. The video will display different types of motion, and describe how certain robot motions map into the 3D configuration space.

Configuration Space Visualization - This is a must watch!